همین طور که میدونید الکترونیک از چندین بخش تشکیل شده که یکیش مبانی دیجیتال یا مدار منطقی که اساس کارش منطقه اره یا نه .
یعنی چی ؟ یعنی این که یا یه چیز وجود داره یا نداره در کل با ولتاژ ۵ ولت یا ۰ ولت کار میکند.
سنسوری به ما می گوید مانعی جلو ما است یعنی پایه خروجی سنسور چند ولت است؟ ۵ ولت
روشن یا خاموش بودن هم به همین صورت نشان میدهند.
البته که همیشه از کلمه ۵ ولت است یا صفر ولت استفاده نمی شود.
نماد ریاضی ۰ و ۱ را در دیجیتال به کار میبریم.
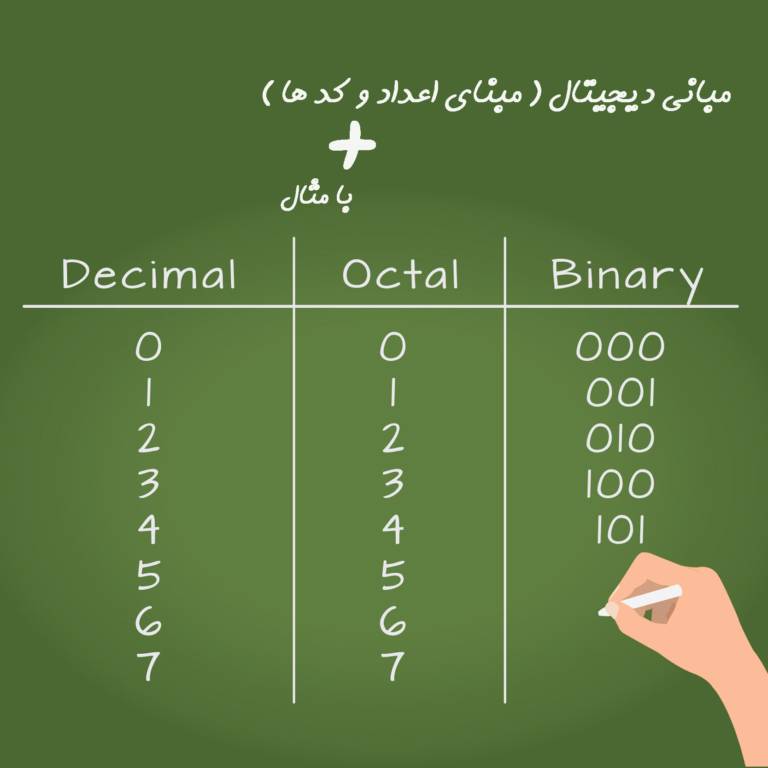
امروز با مبانی اعداد دیجیتال انواع مبنا ها ( سیستم اعداد دیجیتال ) انواع کد های دیجیتال بیشتر آشنا میشیم .
اعداد اعشاری ( ۹ تا ۰ ) مبنای ده دهی – دسیمال
دسیمال یا ده دهی اعدادی هستن که هر روز از انها استفاده میکنیم.
یعنی اعدادی بین ۰ تا ۹ ، در مبنای ۱۰ یا هر مبنایی اعداد هر عدد ارزش خاصی دارد بیشتر براتون توضیح بدم.
(۱۲۴ ) در مبنای ده
| یکی | دهتایی | صد تایی |
| ۴ | ۲ | ۱ |
مابقی سیستم اعداد هم هر عددشون یک ارشی دارد که بیشتر آشنا میشویم
سیستم اعداد باینری یا دو دویی
ارزش عددی در باینری به شرح زیر است
| ۱ | ۲ | ۴ | ۸ | ۱۶ | ۳۲ | ۶۴ | ۱۲۸ | ۲۵۶ | ۵۱۲ |
حالا میخوایم ببینیم عدد ۱۳ در مبنای ده تبدیل به مبنایی دو شود چه شکلی پیدا میکند
برای این کار معمولا از تقسیم های پی در پی استفاده میکنیم
تبدیل اعشاری به باینری
( ۱۱۰۱ ) → ( ۱۳ )
برای رسیدن عدد دسیمال به دو دویی باید تقسیم های متوالی انجام داد تا به نتیجه ۱ یا ۰ برسیم مانند مثال.
مثال :
۱۳/۲=۶
باقیمانده ۱ (عدد چهارم)
جواب تقسیم ۶
۶/۲=۳
باقی مانده ۰ (عدد سوم)
جواب تقسیم ۳
۳/۲=۱
باقی مانده ۱ (عدد دوم)
جواب تقسیم ۱ (عدد اول)
حالا موقع این رسیده که عدد بدست بیاریم جواب تقسیم اخر اولین عدد و بعدی ها باقی مانده ها میشود.
(۱۱۰۱)
مثال : عدد ۱۱ به شکل زیر است .
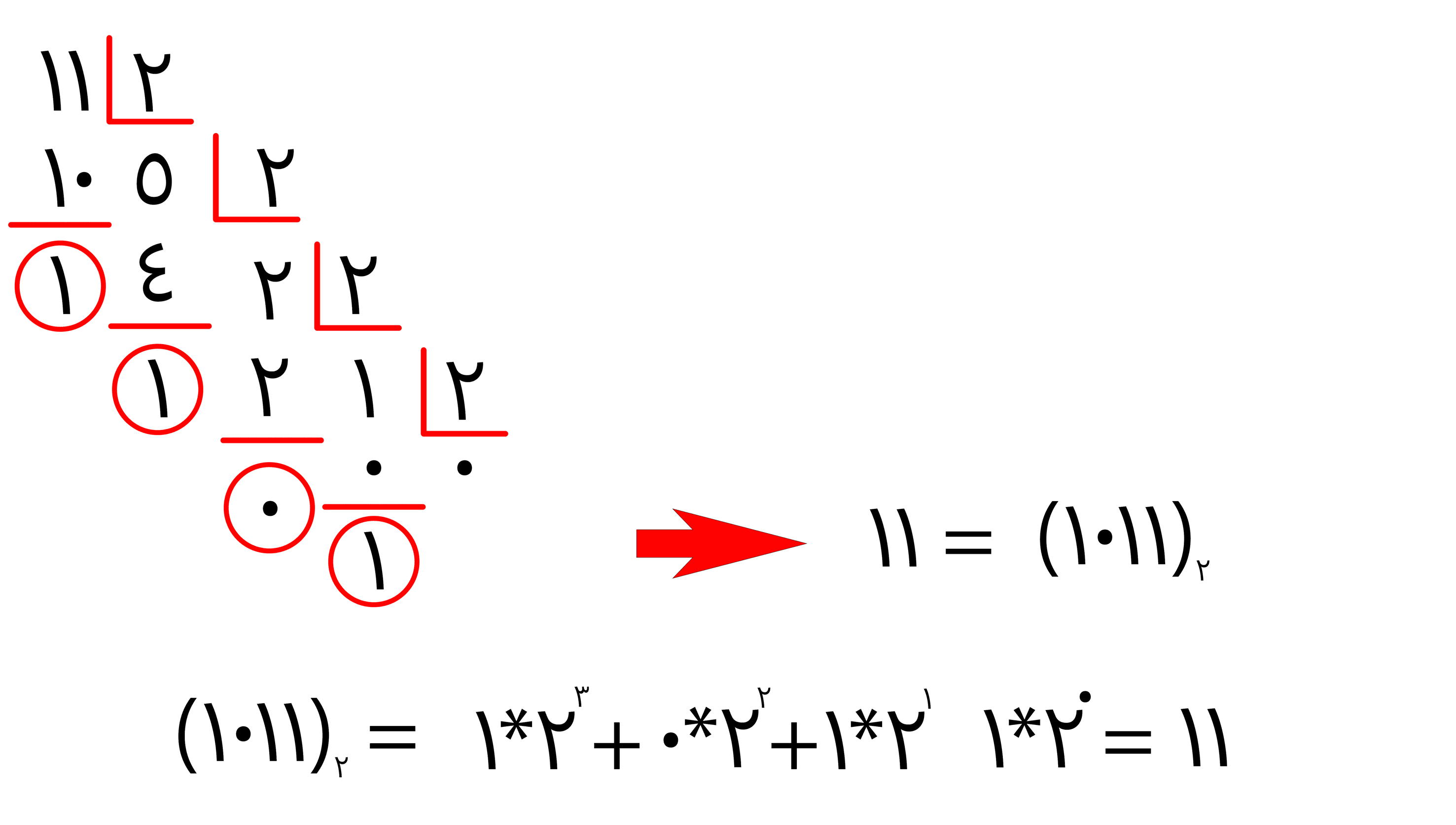
تبدیل باینری به اعشاری
ببنید اینو با یه مثال براتون توضیح میدیم که خیلیییی سریع یاد بگیرید
عدد (۱۱۰۱۱) در مبنایی دو میخوایم ببینیم در مبنای ده چنده
مرحله اول : به تعداد عداد باید جدول بنویسیم بعد عداد را در جایگاه ارزشی خودش بنویسیم
| ۱ | ۲ | ۴ | ۸ | ۱۶ |
| ۱ | ۱ | ۰ | ۱ | ۱ |
مرحله دوم : حالا هر عدد را در جایگاهش ضرب میکنیم و با بعدی جمع
(۱*۱)+(۱*۲)+(۰*۴)+(۱*۸)+(۱*۱۶) = ۲۷
سیستم اعداد اکتان یا هشتایی
ارزش عددی در باینری به شرح زیر است
| ۱ | ۸ | ۶۴ | ۴۰۹۶ |
حالا میخوایم ببینیم عدد ۱۳ در مبنای ده تبدیل به مبنایی هشت شود چه شکلی پیدا میکند
برای این کار معمولا از تقسیم های پی در پی استفاده میکنیم
تبدیل اعشاری به اکتال
( ۱۵) → ( ۱۳ )
برای رسیدن عدد دسیمال به اوکتان باید تقسیم های متوالی انجام داد تا به نتیجه ۷ تا ۰ برسیم مانند مثال.
مثال :
۱۳/۸=۱ (عدد دوم)
باقیمانده ۵ (عدد اول)
حالا موقع این رسیده که عدد بدست بیاریم جواب تقسیم اخر اولین عدد و بعدی ها باقی مانده ها میشود دقیقا به ترتیب باینری.
(۱۵)
تبدیل باینری به اکتال
عدد باینری نوشته سه بیتی از سمت راست سه تا سه تا جدا کرده اگر آخری یک رقم یا دو رقم کم داشت صفر اضافه می کنیم
مثال :
عدد (۱۱۰۱) که میشه ۱۳ میخوایم ببریمش تو اکتال
عدد سه رقم سه رقم از سمت راست جدا میکنیم و اگر رقم اخر 1 یا 2 عدد باقی مانده بود به جای عداد نامجود 0 میگذاریم
(۰۰۱,۱۰۱)
۱۰۱ میشه عدد ۵
۰۰۱ میشه در باینری ۱
عدد بدست امده میشه (۱۵) در مبنای هشت
تبدیل اکتال به اعشاری
ببنید اینو با یه مثال براتون توضیح میدیم که خیلیییی سریع یاد بگیرید دقیقا مثل باینری
عدد (۱۵) در مبنایی هشت میخوایم ببینیم در مبنای ده چنده
مرحله اول : به تعداد عداد باید جدول بنویسیم بعد عداد را در جایگاه ارزشی خودش بنویسیم
| ۱ | ۸ |
| ۵ | ۱ |
مرحله دوم : حالا هر عدد را در جایگاهش ضرب میکنیم و با بعدی جمع
(۵*۱)+(۱*۸) = ۱۳
سیستم اعداد هگز یا شانزده تایی
در این سیستم از ۱۶ عدد وجود دارد ولی از عدد ۹ به بعد از حروف انگیلیسی استفاده شده که در زیر این خط میبینید
| ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | A | B | C | D | E | F |
در جدول زیر ارزش هر جایگاه اعداد در مبنای ۱۶ نمایش میدیم که بسیار مهمه و عدد ۳۵۴ در آن نمایش میدیم
| 1 | 16 | 256 | 65534 |
| 2 | 6 | 1 | 0 |
تبدیل اعشاری به هگز
عدد ۳۵۴ در مبنای ده ، دمبنای ۱۶ به این صورت مینوسیم ۱۶۲
حالا میخوایم ببینیم عدد ۱۳ در مبنای ده تبدیل به مبنایی شانزده شود چه شکلی پیدا میکند
خب ۱۳ جزو اعداد مبنا است پس میشود D یزارید یک مثال بهتر بزنیم با یک روش متفاوت
عدد ۲۶۴ در در مبنای ۱۰ ، مبنای ۱۶ چه شکلی نمایش داده میشود
خب این روشی که الان میگوییم در تمامی سیستم اعداد کاربرد دارد و میشود از ان استفاده کرد پس با دقت بخونید ، همونطور که بالا تر گفتیم در ۱۶ ارزش اعداد ۱ ، ۱۶ ، ۲۵۶ و…
برای تلدیل کردن عدد ۲۵۶ در مبنای ده به ۱۶ باید از بزرگترین ارزش عددی که از خود عدد اصلی کمتر است شروع کرد .
می پرسیم چند تا ۲۵۶ در عدد ۲۶۴ است ؟
جواب میشود ۱
۲۶۴-۲۵۶ = ۸
حالا ۸ باقی ماند از عدد اصلیمون دوباره با ارزش کمتر از خود سوال میپسیم
چند تا ۱۶ تا در ۸ هست ؟
جواب ۰
حال که جواب ۰ شد سوال بعدی با ارزش پایین تر میپرسیم
چنتا ۱ در ۸ است؟
جواب میشود ۸
حالا جواب ها را از اخر به اول مینوسیم
(۱۰۸) در منای ۱۶ مساوی ۲۶۴ در مبنای ۱۰ است
تبدیل باینری به هگز
عددباینری نوشته شده را از سمت راست چهار تا چهار تا تا جدا کرده اگر آخری یک رقم یا دو رقم کم یا سوم داشت صفر اضافه می کنیم
مثال :
عدد (۱۱۰۱) که میشه ۱۳ میخوایم ببریمش تو هگز
(۰,۱۱۰۱) : ۱۳ در مبنای ۱۶ که در واقع باید بنویسیم D
یک مثال دیگر :
عدد (۱۰۱۰۱) که میشه ۲۱ میخوایم ببریمش تو هگز
(۰۰۰۱,۰۱۰۱) : ۵ در ارزش یکی ۱ در ارزش ۱۶ تایی
که جواب میشود ۱۵ در مبنای شانزده.
در مبانی دیجیتال( سیستم اعداد و کدها) ما بیشتر با کدها و اعداد دیجیتال آشنا شدیم که هر کدام در چه قسمتی از کامپیوتر و الکترونیک به کار می رود
و تبدیل کردن اعداد را با هم یاد گرفتیم که این تبدیل ها بیشتر در الکترونیک به کار می رود
امیدوارم از مبانی دیجیتال ( سیستم اعداد و کدها ) لذت برده باشید
در جلسه بعدی با جمع و تفریق ضرب و تقسیم در سیستم های مختلف اعداد بیشتر اشنامیشیم حتما سر به اینستاگرام و تلگرام ما بزنید
_______ _______
مقالات مرتبط
اگر می‌خواهید از آخرین و محبوب‌ترین مقالات ما در ایمیل خود مطلع شوید، همین الان ایمیل و شماره موبایل خود را در کادر زیر وارد کنید: 
با عضویت در ربات افزار میتوانید :